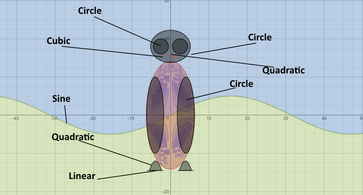
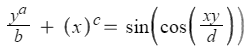Desmos Owl Graph
a. How did you go about drawing this image? (Did you plan? Did you use patterns, reflections of curves? Did you experiment? Did you consult with peers/teacher?) (3-5 sentences)
I originally was inspired to create this image by a strange behavior in desmos I found when using the impossible function, y = sin(xy). I noticed that this pattern created a strange featherlike pattern. Upon further investigation, I began to determine different variables in the function. The resulting function was
I originally was inspired to create this image by a strange behavior in desmos I found when using the impossible function, y = sin(xy). I noticed that this pattern created a strange featherlike pattern. Upon further investigation, I began to determine different variables in the function. The resulting function was
Where a modifies the function's horizontal magnitude, b modifies horizontal magnitude, c modifies the angle of reflection, and d modifies the detail of the function.
b. How did using Desmos and creating this drawing help you understand function families and their transformations? (Be specific and discuss two types of functions and what you learned about them for example, discuss how you understand linear and quadratic functions.) (3-5 sentences)
I really enjoyed investigating elliptical functions such as
(y-18)^2 + (x^2 / 1.5) <= 18.
I strongly believe that experimenting with these variables and being able to visualize them is very helpful. In the example above, (x^2 / 1.5) can be slightly modified to change the width of the circle, by changing a. (x^2 / a). I would never have known this had I not experimented with various functions.
b. How did using Desmos and creating this drawing help you understand function families and their transformations? (Be specific and discuss two types of functions and what you learned about them for example, discuss how you understand linear and quadratic functions.) (3-5 sentences)
I really enjoyed investigating elliptical functions such as
(y-18)^2 + (x^2 / 1.5) <= 18.
I strongly believe that experimenting with these variables and being able to visualize them is very helpful. In the example above, (x^2 / 1.5) can be slightly modified to change the width of the circle, by changing a. (x^2 / a). I would never have known this had I not experimented with various functions.
Tessellation
Tessellations Proccess
To begin this process, I created a new photoshop document. I then drew a basic shape and copied one side of the shape to the other, making the copied side white. Then, I deleted everything within the new white shape, creating a perfect hole for the other shape. I did this for the top and bottom as well as both sides. Finally, I copied the shape and pasted it over and over onto itself.
Response
My tessellation involves translations, both vertically and horizontally. These translations created a very clean and interesting pattern. The pattern exemplifies that art and math, interacting as they so often do, are truly intertwined in many places. In the words of Albert Einstein, "The greatest scientits are always artists as well." A blogger puts it beautifully by simply saying, "Science and Art Go Hand-in-Hand."¹
¹(http://blogs.scientificamerican.com/guest-blog/2012/08/22/from-stem-to-steam-science-and-the-arts-go-hand-in-hand/)
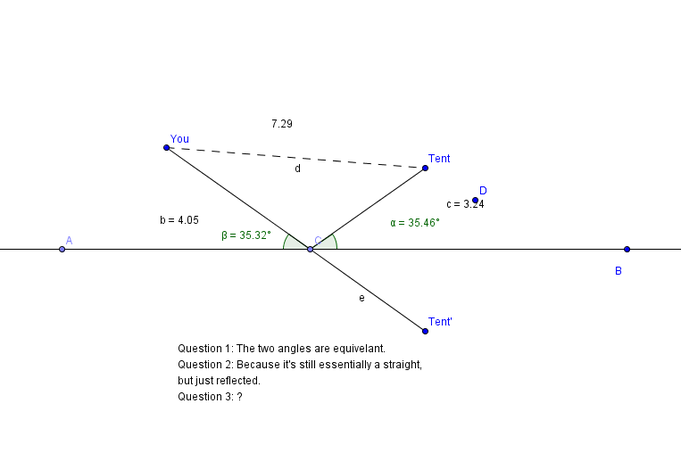
GGB Lab: The Burning Tent
(for some reason I missed question 3 in the picture. The answer to this question is the two lines intersect at point C. This is where you should go to the river.)
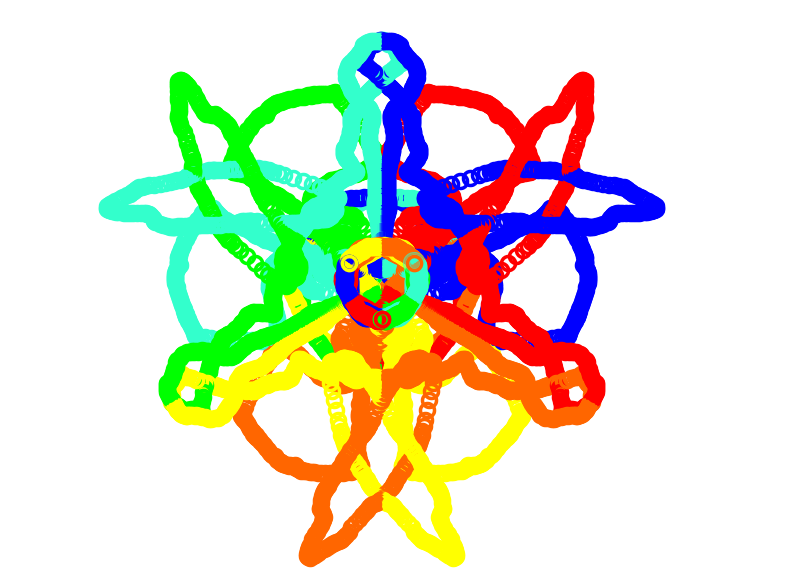
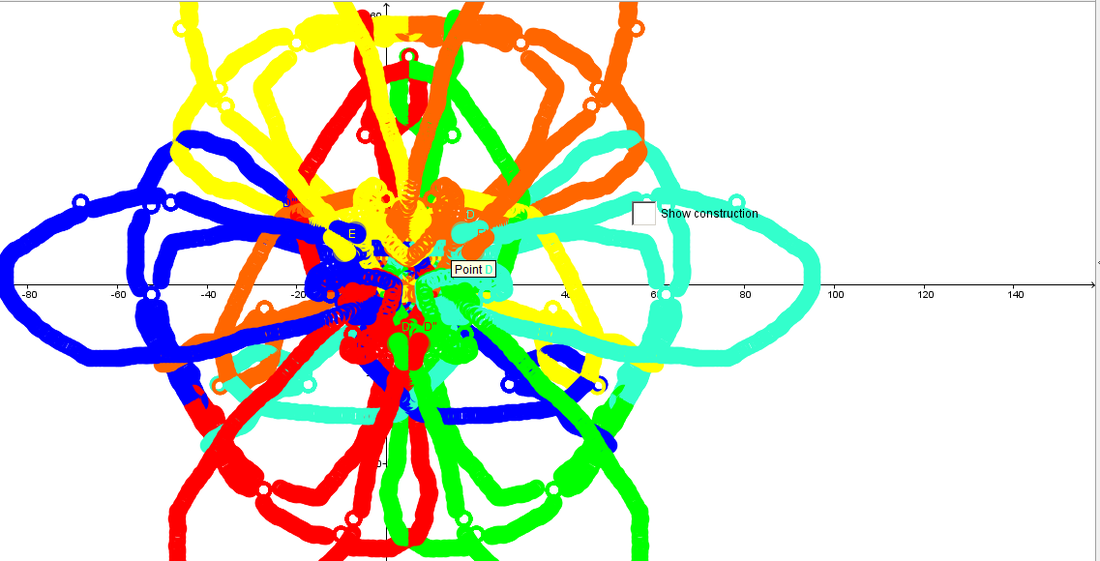
Snail Trails Revised
In this lab we created "snails" and observed the trails they left behind. The snails were just dots reflected across lines dividing a circle. Their trails often end up in roughly hexagonal shapes. These “snails" show rotational symmetry if you ignore the color as well as point symmetry from one point to another. This shape has three lines of rotational symmetry and can be rotated upon itself in three steps of 120°.
Snail Trails
In this lab we created "snails" and observed the trails they left behind. The snails were just dots reflected across lines dividing a circle. Their trails often end up in roughly hexagonal shapes. These “snails" show rotational symmetry if you ignore the color as well as point symmetry from one point to another.